PESERA-DESMICE: Land management evaluation model

Table of Contents

1. Authors
2. Summary
3. Acronyms
4. Introduction
5. Coarse-scale model description
   1. The PESERA model: summary
   2. Alternative approaches to assessing soil erosion
   3. Process representation in PESERA
   4. Extensions of PESERA
   5. Adapting PESERA
   6. Assessment at catchment scales
6. Cost-effectiveness modelling
   1. Step 1
   2. Step 2
   3. Step 3
   4. Step 4
   5. Step 5
   6. Step 6
   7. Step 7
   8. Step 8
   9. Step 9
   10. Step 10
   11. Step 11
   12. Step 12
7. Agent-Based modelling in Spain
   1. Phase 1
   2. Phase 2
   3. Phase 3
   4. Phase 4
   5. Phase 5
   6. Phase 6
8. Input-Output modelling in Spain
   1. Model construction
   2. Scenario analyses
9. References

Process representation in PESERA

Runoff

PESERA represents a fundamental advance on previous models of comparable simplicity, most notably the USLE and its derivatives by explicitly separating hydrology from sediment transport. That is to say that it first estimates storm overland flow runoff, and then uses the runoff to estimate sediment transport. Soil properties therefore enter separately into these two stages, replacing the USLE erosivity, a climatic property, and erodibility, a soil property.

At the same time, the PESERA model has been designed to provide an estimate of long term erosion and must therefore scale up from our knowledge of instantaneous sediment transport, as a function of shear stress or flow power, to firstly an aggregate relationship between event discharge and event sediment discharge, and secondly from single events to the aggregate of storm events across the relevant distribution of storms. This temporal up-scaling provides the essential link between climate, defined by the distribution of rainfall events, and long term sediment transport. Although this scaling up has been discussed and partially implemented in previous models (Kirkby et al., 1996; Kirkby, 1998), it has not previously been applied within a comprehensive soil erosion model.

Precipitation is divided into daily storm events, expressed as a frequency distribution, that drive infiltration excess overland flow and soil erosion, and monthly precipitation, some of which may be as snow, driving saturation levels in the soil. Infiltration excess overland flow runoff is estimated from storm rainfall and soil moisture. Sediment transport is then estimated from overland flow and routed, in principle, downslope. To obtain long term estimates of soil erosion these estimates must then be scaled up by integrating over time. This process of scaling up has two stages, first from momentary to event-integrated dependence, and secondly from events to long term averages via the frequency distribution. For the first stage, if instantaneous sediment discharge can be expressed as a power law dependent on instantaneous water discharge, for example through the Yalin Equation (Finkner et al., 1989). The relationship between event total sediment discharge and event total discharge will, in general, also be a power law, but the exponent will differ according to how hydrograph forms change with flood volume. In this respect, it is intermediate between very short interval sediment transport models and the much coarser time resolution in long term landscape evolution models (e.g. Tucker et al., 2001; Coulthard et al., 2005).

In the second stage of scaling up, individual storm totals are integrated over the frequency distribution of storms. Two assumptions are normally made, first that the distribution of storms can be replaced by the distribution of daily rainfalls, and second that overland flow can be estimated on the basis of monthly average soil moisture conditions. The first of these assumptions avoids the discussion of how rainfall is divided, more or less arbitrarily, into storm events. The use of a daily unit is both convenient, in that daily rainfall data is relatively widely available, and appropriate because bursts of rainfall within a single day are significantly influenced by raised soil moisture levels from previous bursts, whereas for longer periods there may be significant drying between bursts. Similarly, monthly updating of soil moisture is sufficient to reflect important seasonal differences in weather, to respond to seasonal differences in land cover and to make use of widely available meteorological data. These assumptions are, however, a compromise, attempting to simplify the estimation of storm runoff while retaining the frequency signature of storms (daily) and soil moisture (monthly).

This approach can be applied using either an historic (or simulated historic) sequence of daily rainfalls, or by summing over a frequency distribution of daily rainfall events for each month. The former approach is preferable for comparison with observed data, whereas the latter is more suitable for estimating long term average rates: it has the disadvantage that it does not respond to inter-annual differences or to the timing of consecutive storms within a month. These methods thus provide an explicit link to available climatic data, providing an improved physical basis for comparisons across large regions, and with climate scenarios or historic data.

There are a number of simple methods for estimating storm runoff from storm rainfall. Implicitly, these are all based on an understanding of i) the infiltration process, and ii) that erosive overland flow can generally be represented as an infiltration excess, or Hortonian, process. The effect of subsurface flow, where and when it is important, may then be used to modify potential rates of infiltration with lower infiltration under wet conditions. Similarly, the role of vegetation and soil organic matter can modify the infiltration rates through changes in soil structure and/or the development over time of surface or near-surface crusting. Three models are coupled to provide the dynamics of these responses; i) an 'at-a-point' hydrological balance, which partitions precipitation between evapo-transpiration, overland flow, subsurface flow and changes in soil moisture; ii) a vegetation growth model, which budgets living biomass and organic matter subject to the constraints of land use and cultivation choices; and iii) a soil model, which estimates the required hydrological variables from moisture, vegetation and seasonal rainfall history.

'At-a-point' soil hydrology can be described through the Richards' equation, although with reservations where both matrix and macropore flow are active. Solutions may be approximated through the use of infiltration equations, such as the Green-Ampt (1911) or Philip (1957) formulations. However, these approaches are not compatible with the use of daily time steps, within which the detail of storm profiles is lost, and it is impracticable to provide better estimates of runoff than those from the SCS (Soil Conservation Service) curve number (Yuan et al., 2001) or a simple bucket model. Here the bucket model is preferred, which offers a simple conceptual insight into the volume of infiltration before runoff occurs, and can be linked directly to concepts of soil moisture storage, as it varies within and between sites. In the bucket model, runoff r is given by:

(1),

In which R is total storm rainfall, R₀ is the runoff threshold or bucket storage capacity and p is the dimensionless proportion of subsequent rainfall that runs off. All values are normally expressed in mm.

Although there is substantial scatter in relationships between observed total rainfall and runoff, and the bucket model (equation 1) has been adopted in PESERA, as the simplest model and one that is broadly consistent with these data, in which storms are treated as independent random events. Comparison with a more detailed model, based on the Green-Ampt equation, shows a similar scatter for daily rainfall totals over a set of storm events taken from a continuous record for a semi-arid area in SE Spain. Equation (1) has been freely fitted to the data and it can be seen that, without a more detailed knowledge of storm profiles than can be derived from the daily record, it is both impracticable to apply a more sophisticated model, and unwise to make runoff forecasts for any individual storm.

Soil Water

Water infiltrating into the soil is limited by the runoff threshold, which is conceptualized as an available near-surface water store. The upper limit for this store is constrained by soil properties, and is currently estimated from mapped soil classes in the European Soil Database (King et al., 1995). This store may be decreased where the soil is crusted, and/or if subsurface flow brings saturated conditions close to the surface. Additional considerations apply where the soil is frozen or snow covered. Both sub-surface flow and the near-surface water store are available for evaporation and for evapo-transpiration linked to plant growth. Soil properties have, necessarily, been taken from existing soil maps, since details of the primary properties required are not available at a European scale. Data have been derived from the European Soil Database, giving estimates of available water storage capacity, crustability and erodibility (as defined by k in equation 8 below). The pedo-transfer rules used have been closely modelled on work by Le Bissonnais et al. (2002, 2005) and Cerdan et al. (2002), with modification described by Gobin et al. (2004) and Jones et al. (2000). It is recognised that soil maps are an imperfect source of data, but are unlikely to be superseded in the near future.

After allowing for interception, evapo-transpiration is partitioned between the vegetated and un-vegetated fractions of the surface according to the proportional vegetative crown cover. Interception is calculated as a fraction of rainfall rather than a fixed capacity, and this fraction increases with vegetation biomass (Llorens et al., 1997). Each evapo-transpiration component is associated with a rooting depth (e.g. Shah et al., 2007) according to the land cover type for the vegetated area and normally set at 10mm for the bare soil. For each component, potential evaporation (PE), after subtraction of interception, is then reduced exponentially to an actual rate (AE) of:

(2)

Where

• WUE = dimensionless water use efficiency for stage of plant growth (or 1.0 for bare soil)
• D is saturated subsurface deficit (mm) and
• h_R is the rooting depth (mm of water) for each partition.

Contributions to evaporation (in mm per measurement period) are weighted for the fractional plant cover to give a combined estimate.

Subsurface flow is estimated using TopModel (Beven & Kirkby, 1979), with topographic properties estimated from local relief (from DEM) and soil characteristics (saturated hydraulic conductivity and TopModel soil parameter, m) from the soil type, based on field experience (e.g. Beven et al., 1984). The average saturated deficit is estimated in monthly steps to provide the background hydrological conditions and, in particular, the saturation constraint on the runoff threshold which controls overland flow runoff in each storm. Deficit is updated monthly from the TopModel expression:

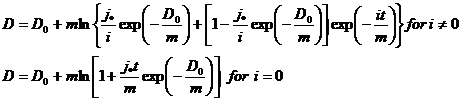(3)

where

• D is the deficit after time t (as in equation 2)
• D₀ is the initial deficit (mm),
• i is the net rainfall intensity (mm/month)
• m is the TopModel soil parameter (mm), and
• j_* is the average saturated runoff rate (mm/month)

This expression also estimates the net subsurface runoff over the month as

(4)

In these calculations the total net rainfall is used, corrected for the overland flow runoff where this is a significant fraction is used. Where the deficit falls below zero, the negative deficit is re-calculated as saturation overland flow.

This combination of an infiltration excess mechanism, represented by the bucket model, with a saturation excess mechanism, represented by TopModel, provides a robust hydrological sub-model which provides an adequate response across the humid to semi-arid continuum. As shown below, the evapo-transpiration stream is also used to drive a simple plant growth model, which is also responsive to this range of conditions.

The runoff threshold for infiltration excess overland flow is estimated as an area-weighted average of the thresholds under vegetation and in the bare gaps between. Under vegetation, rainfall is lost to interception, and the runoff threshold is calculated as the lesser of two values:

1. available near-surface water storage capacity (depending on soil textural properties), or
2. the sub-surface saturation deficit (from the TopModel estimate described above).

In arable areas, surface roughness represents the full storage capacity of furrows immediately after ploughing, and this decays exponentially with time in the subsequent period, eventually falling to a minimum value representing the textural roughness of the surface (Darboux et al, 2002; le Bissonnais et al., 2005. Naturally vegetated areas are also assumed to present this minimum roughness.

Bare areas are also considered to be subject to crusting, with a tendency to crusting referred to mapped soil classes, largely interpreted in textural terms as a minimum runoff threshold for a fully crusted surface (Le Bissonnais et al., 2002, 2005). For arable areas, the runoff threshold for a bare area is re-calculated as beneath vegetation immediately after tillage, and this decays exponentially towards the minimum for each soil type with accumulated monthly rainfalls.

This formulation provides a seasonal response in runoff thresholds, and therefore in infiltration excess overland flow. For a conventionally ploughed annual crop, for example, thresholds are high on first planting, but fall very rapidly immediately afterwards, particularly if there is rain, as crusting develops while the crop provides little cover. As the crop grows, the runoff threshold recovers, reaching high values as the crop matures. After harvest these high values fall again, depending on how or whether the surface is protected. Under natural vegetation there is much less annual variation, with runoff thresholds responding to the seasonality of cover.

The distribution of runoff and erosion over storms

Storm rainfalls are considered as independent random events, defined by a frequency distribution for each month of the year. The autocorrelation between successive events is weakly represented by the seasonal variations in soil moisture, but there is some loss of information by using this approach. This represents a trade-off between simplicity and accuracy, with the least impact on estimates for the semi-arid areas where soil erosion is generally considered to be most severe, because soils normally dry out between major events.

As noted above, daily rainfall totals have been used as the basis for analysis because, while recognizing the limitations of this approach, it allows the use of the widespread daily precipitation data. On a month by month basis, daily rainfall is analyzed to give monthly total, mean rain per rain-day and the standard deviation of rainfalls on rain-days. These statistical moments allow fitting most observed data for daily rainfalls to the probability density function for a Gamma distribution as follows:

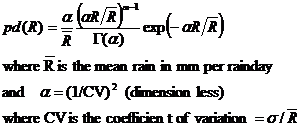(5)

The gamma distribution provides a robust fit (e.g. McSweeney, 2007), giving a good balance between small and large events. The CV is generally between zero and unity, so that the probability density distributions peak at zero rainfall.

Infiltration excess overland flow for a storm of rainfall R is then given by equation (1) above, and the total overland flow runoff for the month integrated numerically as:

(6)

This is used directly as a component of the water balance, but it will be seen below that a power of event runoff is used to estimate sediment transport. For a power law of 2.0, the corresponding summation of (Runoff)² then takes the form:

(7),

Comparable expressions are required if other integral powers are used. This then gives the correct strong weighting to the largest events in the accumulated total.

Land use and vegetation cover

The hydrological components of the model, as described above, are strongly dependent on vegetation cover, which is understood to be a major control on both runoff and erosion. For Mississippi Loess soils, measured runoff on bare soil exceeds 80%, and falls to 2% under a dense vegetation cover, and this 40-fold difference in runoff gives a 2000-fold difference in sediment loss (Meginnis, 1935). Other experiments (e.g. Hudson and Jackson, 1959) have shown that fine netting stretched above the surface of an agricultural field has almost as strong an effect as dense vegetation in reducing runoff and erosion. Thus the importance of crown cover for both runoff and erosion is extremely strong, although it is recognised that root and soil organic matter effects are also important for uncultivated areas (e.g. Kirkby and Morgan, 1978).

Input of land cover data has been approached in the model through two alternative strategies, each of which has its advantages: first through direct remote sensing of land cover and second through modelling vegetation growth. Geomatic data has the advantage that it provides a direct measure of real vegetation abundance, which is now available monthly for a period of over twenty years, through AVHRR and LANDSAT images. This integrates the effects of all impacts on the cover in an unambiguous historical record. It therefore includes the impacts of factors which may not all be fully incorporated in a model. However, the analysis is based on the best of three monthly satellite passes, and suffers from the persistence of cloud cover in Northern Europe and other humid areas. It also lacks any direct forecasting potential, and therefore has limited applicability for analyses of scenarios for land use and/or climate change.

Vegetation growth models are well established, with both generic and crop-specific models (e.g. White et al., 2005). The models applied here have been based on a biomass carbon balance for both living vegetation and soil organic matter. Such models may be insufficiently parameterized to cover the full range of functional types, and are commonly limited by absence or inadequate representation of some processes. Fire and grazing are, for example, not directly represented in the models that have been used to date with PESERA. As a result, the vegetation cover is more a 'potential' than actual cover, with only indirect parameterization of some relevant influences. However, growth models respond directly to changes in land use or climate drivers, and so have greater scenario testing potential.

Analysis of RS images can be based directly on NDVI, but improved results have been obtained using the satellite-derived surface temperature to correct for water content, linearly un-mixing in a phase-space triangle between water, vegetation and soil. This gives a measure of vegetation abundance, which can be empirically related to cover and/or above ground biomass, and from which some land use classes can be interpreted from the seasonal cover cycle. (Haboudane et al., 2002).

The generic vegetation model estimates gross primary productivity (GPP) as being proportional to the actual transpiration from the plant. This is offset by respiration, at a rate increasing exponentially with temperature and proportional to biomass. Leaf fall fraction is a decreasing function of biomass, to allow for a larger structural component in large plants. Where respiration is greater than GPP, a 'deciduous' response increases an additional leaf fall at a rate that increases with temperature. Finally the modelled vegetation biomass is allowed to lose a fraction to grazing or plant gathering activities. The vegetation is protected from complete elimination by allowing only a fraction to be consumed, and this also relates grazing consumption to availability.

Soil organic matter is increased by leaf fall, except where crops are harvested, and decomposes as a single linear store at a rate that increases with temperature.

Cover is calculated independently, with reference to an equilibrium cover defined as the ratio of plant transpiration to potential evapo-transpiration rate. Cover converges on this (changing) equilibrium value at a rate which is larger where biomass is small, and is the variable which drives the seasonal partition of runoff threshold between vegetated and bare areas. This generic model has been calibrated against global distributions of biomass (Kirkby and Neale, 1987). Crop models are variants of this generic model, with additional controls through data on regional patterns of planting and harvest dates, and with an evolution of water use efficiency through the life cycle of the crop (Gobin and Govers, 2003).

Sediment transport and sediment yield

Runoff generated locally may not reach the base of the slope to deliver sediment to a channel, and the runoff coefficient for infiltration excess overland flow has therefore generally been observed to decrease with distance or area downslope. Summed over the distribution of storm sizes described above, these factors lead to a less then linear increase of discharge with distance downslope, and this has generally been represented as a logarithmic or power law (with exponent ~ 2/3) relationship (Kirkby et al., 2005).

Estimates of sediment transport are based on infiltration excess overland flow discharge which has been discussed above. Most sediment transport equations are based on considerations of tractive stress or flow power, and commonly generalized into a power law in discharge and gradient, thus avoiding a more detailed analysis of flow thread geometry. The commonest formulations (e.g. Musgrave 1947) assume that there is an ample sediment supply,and that sediment is everywhere transported by soil erosion at its transporting capacity per unit flow width C (kg.m^-1day^-1), expressed in the form:

(8)

Where

• k is the soil erodibility,
• q is the overland flow discharge per unit flow width (l.m^-1d
• Λ is the local slope gradient (dimensionless),and
• m, n are empirical exponents, generally in the ranges m = 1.5-3; n = 1-2.

The units for erodibility depend on the exponent m, for example being kg.l^-2.m.day for m =2. In such expressions, discharge is generally associated with distance from the divide, possibly with a change in the exponent m. It has generally been found that the performance of erosion models is remarkably insensitive to the choice of exponents, largely because slope and distance tend to change together, particularly along the upper concavity of a slope profile.

Evaluation of appropriate exponents may be made at a range of time and space scales (e.g. Kirkby et al., 2003). The most direct approach is through soil erosion plots, but these are often not corrected for the frequency distribution of storms to provide meaningful long term averages. A second approach is to look at the critical areas required to support an ephemeral gully formed in a particular storm. This approach requires an analysis of the stability of small depressions, as a balance is reached between infilling by diffusive processes, primarily rainsplash in relevant contexts and their enlargement by soil erosion (rillwash) processes. A third approach is by back analysis of hillslope profile form, which is formed over a period in response to the full distribution of events. The difficulty with this latter approach lies in uncertainty about whether the observed landscape form has developed under process conditions that are still current, or are inherited from conditions of different climate and/or land cover.

Exponent values of m = 2, n = 1 have been adopted here, with computational advantages that are evident below. These values lie within the empirical range, and facilitate the creation of a consistent coarse scale model. Hence for transporting capacity C, it is proposed that:

(9)

where

• r is the local runoff in mm for each event, from equation (1) above,
  and
• x is the distance from the divide (m), so that the term rx is replacing discharge, q in equation (8) above.

Summing over the frequency distribution of daily storm events in any month, the mean total sediment transport takes the form:

(10)

in which the final term may be taken from equation (7) above.

Alternatives to this composite power law approach can simulate selective transportation of different grain sizes, for example by defining transport capacity as the product of detachment rate and travel distance. This approach has the advantage of allowing a spectrum of responses, from a strictly transport limited approach for the coarser soil fractions, to a detachment or supply limited approach for the finest material. Although this latter approach has merit, there are not sufficient data to properly parameterize it for the proposed coarse scale model. In practice this means that the erodibility of fine soils must implicitly be reduced to allow for the limited rate of supply, whether through hydraulic erosion or through removal of previously detached material, and that, for rangeland, selective transportation creates an armour layer over time that reduces erosion rates.

In the PESERA model, sediment transport is interpreted as the mean sediment yield delivered to stream channels and includes no allowance for downstream routing within the channel network. Sediment Yield Y (kg.m^-2a^-1) is the sediment transported to the slope base, averaged over the slope length, that is:

(11)

where the suffix B indicates evaluation at the slope base, the summation is taken over the frequency distribution of daily events in an average year and L = x_B is the total slope length (m).

The term LΛ_B can be expressed, in terms of the total slope relief in metres, , where is the average slope gradient from crest to base, giving:

(12)

Where is the ratio of slope base to average gradient, a number that generally lies between 0.5 and 1.0 for typical convexo-concave slopes. This correction term can be included where available, but generally defaults to a slight correction in the empirical value for erodibility, k.

Equations (11) and (12) are taken as the final form of the expression used in the PESERA model which includes three terms:

1. Soil erodibility, which is derived from soil classification data, primarily interpreted as texture (Le Bissonnais et al., 2002).
2. Local relief, which is derived from DEM data as the standard deviation of elevation within a defined radius around each point.
3. An estimate of accumulated (runoff)², which is derived from a biophysical model that combines the frequency of daily storm sizes with an assessment of runoff thresholds based on seasonal water deficit and vegetation growth.